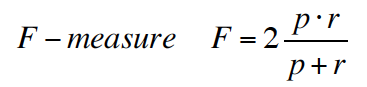Linear Discriminators
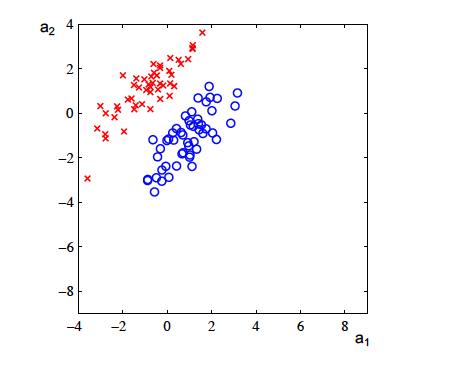
Imagine we have two clusters of points (see figure below) to classify. How do you do it?
Linear Regression
Simple linear regression: a very straightforward simple linear approach for predicting a quantitative response Y on the basis of a single predictor variable X. It assumes that there is approximately a linear relationship between X and Y. Mutiple linear regression: a better approach is to extend the simple linear regression model so that it can directly accommodate multiple predictors. Polynomial regression: in some cases, the true relationship between the response and the predictors may be nonlinear.
Why use a linear regression model?
- it is well undrestood
- it is inherited from statisticians (many ways to evaluate and diagnose)
- it uses a closed-form formula to compute the solution
- the result is very easy to interpret
The linear regression model - super easy!
Assumptions: The observed response (dependent) variable (y) is the true function f(x) with additive Gaussian noise (e) with a mean of 0.
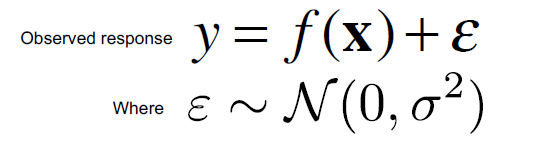
Translate it to english: The expected value of the response variable should be a linear combination of k independent attributes/features.
Hypothesis Space: the set of linear functions (hyperplanes)
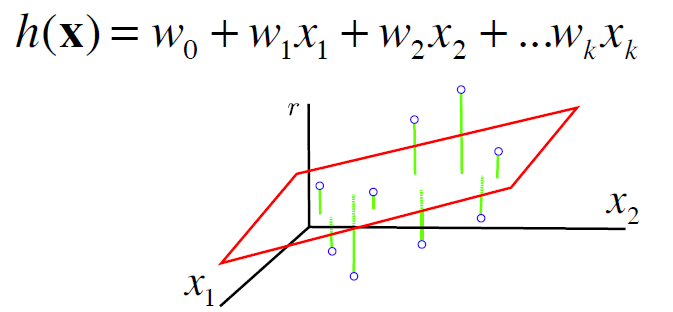
Then, the goal is to find the weights of a function
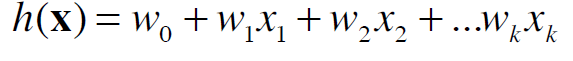
that minimize the sum of squared residuals
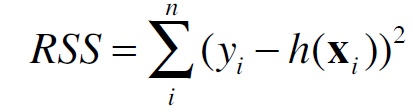
It turns out we have a close-form solution for this question
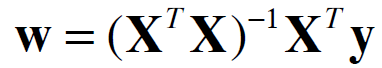
If you are interested in the derivation of this close-form solution, please check it here
Moving from linear regression to linear classifer…
Regression: learning a function to map from a n-tuple to a continuous value.
Classification: learning a function to map from a n-tuple to a discrete value from a finite set
To clean a linear classifer, what we have to do: 1) Label each class by a number 2) Call that number the response variable 3) Analytical derive a regression line 4) Round the regression output to the nearest label number
Potential Problems of regression
1) Non-linearity of the response-predictor relationships 2) Correlation of error terms 3) Non-constant variance of error terms 4) Outliers 5) High-leverage points 6) Collinearity
Perceptron
The perceptron algorithm assigns the initial weights randomly and traverse all the input points to compute the sum of weighted inputs for each point. If the sum of weighted input is larger than the threshold (often times 0), the perceptron algorithm will assign it to be 1 (activated), otherwise 0 (deactivated). If all the predicted output is the same as the desired output, then the performance is considered satisfactory and no changes to the weights are made; otherwise the weighs need to be hanged to reduce the error.
The termination conditions are 1) find the satisfactory weights successfully or 2) the algorithm exceeds the maximum iteration.
The decision boundary
g(x) = wTx
The classification function
h(x) = 1 (if g(x) > 0)
h(x) = -1 (otherwise)
The weight update algorithm
w = some random setting
Do for (certain amount of iterations)
k = (k+1)mod(m)
if h(x_k) != y_k
w = w + xy
Until Vk, h(x_k) = y_k
The termination conditons are: 1) find the linearly separable function (weights); 2) exceed the iterations but do not find the linearly separable function.
Nearest Neighbor Classifier
The basic idea:
- Get some example set of cases with known outputs
- When seeing a new case, assign its output to be the same as the most similar known case. (Then the question becomes: How do you define the most similar known case??)